Graniastosłupy – wzory i przykłady zadań
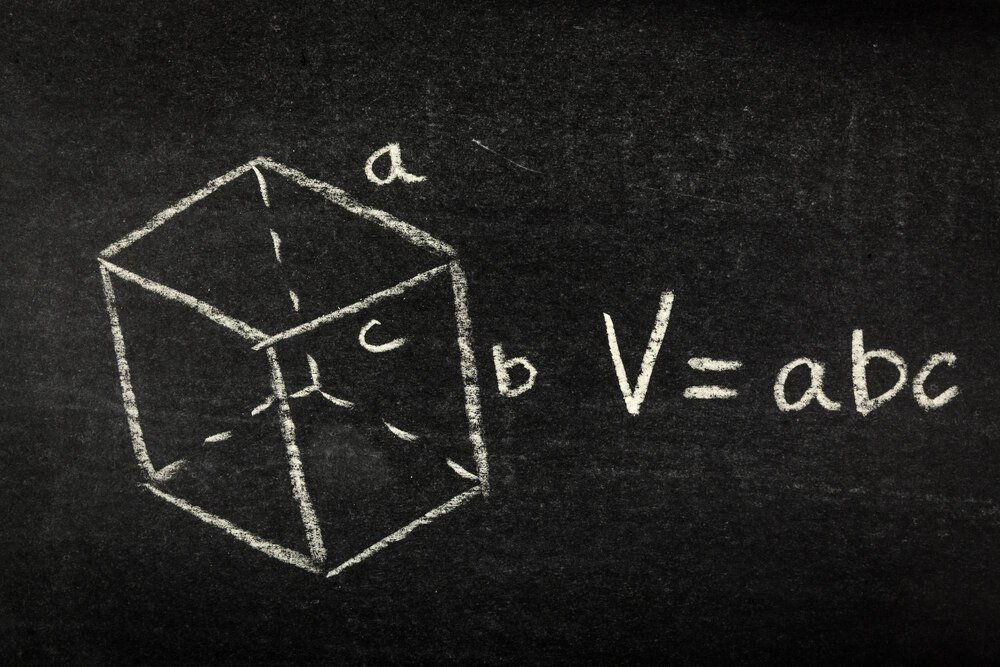
Graniastosłupy pojawiają się w zadaniach z geometrii już w szkole podstawowej, a mimo to wielu uczniów ma z nimi kłopot. Poniżej znajdziesz spokojne, krok po kroku wyjaśnienie, czym jest graniastosłup, jakie ma elementy, jakie są wzory na objętość i pola oraz jak rozwiązywać typowe zadania z graniastosłupów.
Co to jest graniastosłup?
Graniastosłup to bryła, której:
- dwie ściany są identycznymi, równoległymi wielokątami – nazywamy je podstawami,
- pozostałe ściany są prostokątami (w graniastosłupie prostym) lub ogólnie równoległobokami (w graniastosłupie pochyłym),
- wszystkie krawędzie boczne są równoległe i mają taką samą długość.
Jeśli podstawą jest np. trójkąt, mamy graniastosłup trójkątny, jeśli czworokąt – czworokątny itd.
Elementy graniastosłupa
Dla każdego graniastosłupa rozróżniamy:
- podstawy – dwa takie same wielokąty (np. dwa identyczne trójkąty),
- ściany boczne – prostokąty (prosty) lub równoległoboki (pochyły),
- krawędzie podstaw – boki wielokąta będącego podstawą,
- krawędzie boczne – odcinki łączące odpowiadające sobie wierzchołki podstaw,
- wysokość graniastosłupa – długość krawędzi bocznej w graniastosłupie prostym lub odległość między płaszczyznami podstaw w ogólności.
Często używamy dwóch skrótów:
- \(P_p\) – pole podstawy,
- \(P_b\) – pole powierzchni bocznej,
- \(P_c\) – pole powierzchni całkowitej (bocznej + obu podstaw).
Rodzaje graniastosłupów
W szkole najczęściej spotykasz:
- Graniastosłup prosty – krawędzie boczne są prostopadłe do podstaw, ściany boczne są prostokątami.
- Graniastosłup pochyły – krawędzie boczne są nachylone, ściany boczne są równoległobokami.
- Graniastosłup prawidłowy – jest prosty, a jego podstawa jest wielokątem foremnym (wszystkie boki i kąty podstawy są równe), np. prawidłowy graniastosłup sześciokątny.
- Prostopadłościan – szczególny przypadek graniastosłupa prostego o podstawie prostokąta (często wszystkie krawędzie prostopadłe parami).
Podstawowe wzory na graniastosłupy
Najważniejsze wielkości, które obliczamy:
- Objętość \(V\),
- Pole powierzchni bocznej \(P_b\),
- Pole powierzchni całkowitej \(P_c\).
Wzory ogólne
Nie zależnie od typu graniastosłupa (prostego czy pochyłego) obowiązuje:
\[ V = P_p \cdot h \]
czyli: objętość = pole podstawy × wysokość.
Dla graniastosłupa prostego:
- Pole powierzchni bocznej:
\[ P_b = O_p \cdot h \]
gdzie \(O_p\) to obwód podstawy (suma długości wszystkich boków podstawy).
- Pole powierzchni całkowitej:
\[ P_c = P_b + 2P_p = O_p \cdot h + 2P_p \]
Tabela – najczęściej używane wzory
| Rodzaj graniastosłupa | Pole podstawy \(P_p\) | Objętość \(V\) | Pole boczne \(P_b\) | Pole całkowite \(P_c\) |
|---|---|---|---|---|
| Ogólny graniastosłup | \(P_p\) – dane w zadaniu lub liczone osobno | \(V = P_p \cdot h\) | \(P_b = O_p \cdot h\) (dla prostego) | \(P_c = 2P_p + O_p \cdot h\) |
| Graniastosłup trójkątny | \(P_p = \frac{a \cdot h_a}{2}\) lub inne wzory na pole trójkąta | \(V = P_p \cdot H\) | \(P_b = (a+b+c) \cdot H\) | \(P_c = 2P_p + (a+b+c) \cdot H\) |
| Prostopadłościan | \(P_p = a \cdot b\) | \(V = a \cdot b \cdot c\) | \(P_b = 2(a \cdot c + b \cdot c)\) | \(P_c = 2(ab + ac + bc)\) |
W prostopadłościanie zwykle oznaczamy długości krawędzi jako \(a\), \(b\), \(c\).
Graniastosłup prosty krok po kroku – jak liczyć?
W większości szkolnych zadań mamy graniastosłupy proste, więc przyjmijmy to jako standard.
- Zidentyfikuj podstawę – zobacz, jakim wielokątem jest podstawa (trójkąt, prostokąt, sześciokąt foremnny itd.).
- Oblicz pole podstawy \(P_p\) korzystając z odpowiedniego wzoru (np. prostokąt: \(P = a \cdot b\), trójkąt: \(P = \frac{a \cdot h_a}{2}\)).
- Od znajdź wysokość \(h\) graniastosłupa (nie myl z wysokością w trójkącie w podstawie).
- Oblicz objętość używając wzoru \[ V = P_p \cdot h. \]
- Jeśli trzeba policzyć pola powierzchni:
- oblicz obwód podstawy \(O_p\),
- policz \(P_b = O_p \cdot h\),
- policz \(P_c = 2P_p + P_b\).
Typowe błędy i jak ich uniknąć
- Mieszanie wysokości – w graniastosłupie trójkątnym mamy wysokość w podstawie (np. \(h_a\) w trójkącie) oraz wysokość graniastosłupa \(H\). To różne rzeczy.
- Pole a obwód – do objętości potrzebne jest pole podstawy, do pola bocznego – obwód podstawy. Nie zamieniaj ich miejscami.
- Jednostki – jeśli długości są w cm, to pole jest w \(\text{cm}^2\), a objętość w \(\text{cm}^3\). Zawsze zapisuj jednostkę przy odpowiedzi.
Przykłady zadań – graniastosłupy
Przykład 1 – objętość prostopadłościanu
Treść: Prostopadłościan ma wymiary: \(a = 5\,\text{cm}\), \(b = 3\,\text{cm}\), \(c = 8\,\text{cm}\). Oblicz jego objętość.
Rozwiązanie krok po kroku:
- Prostopadłościan to szczególny graniastosłup, więc stosujemy wzór:
\[ V = a \cdot b \cdot c. \] - Podstawiamy:
\[ V = 5\,\text{cm} \cdot 3\,\text{cm} \cdot 8\,\text{cm} = 120\,\text{cm}^3. \]
Odpowiedź: \(V = 120\,\text{cm}^3\).
Przykład 2 – graniastosłup trójkątny, pole podstawy danym wzorem
Treść: Podstawą graniastosłupa prostego jest trójkąt o podstawie \(a = 6\,\text{cm}\) i wysokości opuszczonej na tę podstawę \(h_a = 4\,\text{cm}\). Wysokość graniastosłupa wynosi \(H = 10\,\text{cm}\). Oblicz objętość graniastosłupa.
Rozwiązanie:
- Najpierw liczymy pole podstawy \(P_p\) – pole trójkąta:
\[ P_p = \frac{a \cdot h_a}{2} = \frac{6\,\text{cm} \cdot 4\,\text{cm}}{2} = \frac{24\,\text{cm}^2}{2} = 12\,\text{cm}^2. \] - Objętość graniastosłupa:
\[ V = P_p \cdot H = 12\,\text{cm}^2 \cdot 10\,\text{cm} = 120\,\text{cm}^3. \]
Odpowiedź: \(V = 120\,\text{cm}^3\).
Przykład 3 – pole boczne i całkowite graniastosłupa prostego
Treść: Podstawą graniastosłupa prostego jest prostokąt o bokach \(a = 4\,\text{cm}\) i \(b = 7\,\text{cm}\). Wysokość graniastosłupa wynosi \(h = 9\,\text{cm}\). Oblicz:
- pole powierzchni bocznej \(P_b\),
- pole powierzchni całkowitej \(P_c\),
- objętość \(V\).
Rozwiązanie:
- Obwód podstawy (prostokąta):
\[ O_p = 2a + 2b = 2\cdot4\,\text{cm} + 2\cdot7\,\text{cm} = 8\,\text{cm} + 14\,\text{cm} = 22\,\text{cm}. \] - Pole boczne:
\[ P_b = O_p \cdot h = 22\,\text{cm} \cdot 9\,\text{cm} = 198\,\text{cm}^2. \] - Pole podstawy (prostokąta):
\[ P_p = a \cdot b = 4\,\text{cm} \cdot 7\,\text{cm} = 28\,\text{cm}^2. \] - Pole całkowite:
\[ P_c = 2P_p + P_b = 2\cdot28\,\text{cm}^2 + 198\,\text{cm}^2 = 56\,\text{cm}^2 + 198\,\text{cm}^2 = 254\,\text{cm}^2. \] - Objętość graniastosłupa:
\[ V = P_p \cdot h = 28\,\text{cm}^2 \cdot 9\,\text{cm} = 252\,\text{cm}^3. \]
Odpowiedź: \(P_b = 198\,\text{cm}^2\), \(P_c = 254\,\text{cm}^2\), \(V = 252\,\text{cm}^3\).
Przykład 4 – zadanie „odwrotne” (szukanie wysokości)
Treść: Objętość graniastosłupa prostego o podstawie w kształcie prostokąta wynosi \(V = 360\,\text{cm}^3\). Bok prostokąta ma długość \(a = 6\,\text{cm}\), drugi bok \(b = 5\,\text{cm}\). Oblicz wysokość graniastosłupa.
Rozwiązanie:
- Pole podstawy:
\[ P_p = a \cdot b = 6\,\text{cm} \cdot 5\,\text{cm} = 30\,\text{cm}^2. \] - Wzór na objętość:
\[ V = P_p \cdot h. \]
Z tego:
\[ h = \frac{V}{P_p}. \] - Podstawiamy dane:
\[ h = \frac{360\,\text{cm}^3}{30\,\text{cm}^2} = 12\,\text{cm}. \]
Odpowiedź: wysokość graniastosłupa wynosi \(12\,\text{cm}\).
Prosty kalkulator objętości i pola graniastosłupa prostego
Poniższy kalkulator pozwala szybko obliczyć objętość i pole powierzchni całkowitej graniastosłupa prostego, jeśli znasz:
- pole podstawy \(P_p\),
- obwód podstawy \(O_p\),
- wysokość graniastosłupa \(h\).
Używane wzory:
\[ V = P_p \cdot h \]
\[ P_c = 2P_p + O_p \cdot h \]
Kalkulator graniastosłupa prostego
Jak samodzielnie trenować zadania z graniastosłupów?
Aby dobrze opanować graniastosłupy w matematyce, warto:
- rysować bryłę (nawet schematycznie) – łatwiej zobaczyć, co jest podstawą, a co wysokością,
- zawsze zapisywać wzór przed podstawieniem liczb,
- zaznaczać jednostki przy każdym wyniku pośrednim i końcowym,
- próbować zadań „odwrotnych” – np. z objętości obliczyć wysokość lub pole podstawy.
Po opanowaniu kilku podobnych przykładów zobaczysz, że zadania z graniastosłupów mają bardzo podobny schemat i stają się dużo prostsze.

 Tablice matematyczne PDF – skąd legalnie pobrać?
Tablice matematyczne PDF – skąd legalnie pobrać?  Kalkulator macierzy – działania na macierzach krok po kroku
Kalkulator macierzy – działania na macierzach krok po kroku  Kalkulator całek – szybkie obliczanie całek online
Kalkulator całek – szybkie obliczanie całek online  Kontekst w rozprawce – jak go dobrze wykorzystać?
Kontekst w rozprawce – jak go dobrze wykorzystać?  Powstanie styczniowe – przyczyny, przebieg, skutki
Powstanie styczniowe – przyczyny, przebieg, skutki  Ile jest minut w dobie?
Ile jest minut w dobie?  Mądre życzenia na Dzień Mężczyzny – głębokie i inspirujące sentencje
Mądre życzenia na Dzień Mężczyzny – głębokie i inspirujące sentencje  Niepotrzebna – razem czy osobno i w jakich sytuacjach?
Niepotrzebna – razem czy osobno i w jakich sytuacjach?  Niedobrze – razem czy osobno w różnych kontekstach?
Niedobrze – razem czy osobno w różnych kontekstach?  Dobrze płatne zawody bez studiów – lista i wymagania
Dobrze płatne zawody bez studiów – lista i wymagania  Jak napisać dobre CV, które przyciągnie rekrutera?
Jak napisać dobre CV, które przyciągnie rekrutera?  Harakter czy charakter – która forma jest poprawna?
Harakter czy charakter – która forma jest poprawna?  Przede wszystkim – razem czy osobno w zdaniu?
Przede wszystkim – razem czy osobno w zdaniu?  Koleżankom czy koleżanką – którą formę wybrać?
Koleżankom czy koleżanką – którą formę wybrać?  Gorzej czy gożej – jak to się pisze?
Gorzej czy gożej – jak to się pisze?  W końcu czy wkońcu – która forma jest poprawna?
W końcu czy wkońcu – która forma jest poprawna?  Dołączam czy dołanczam – poprawna forma czasownika
Dołączam czy dołanczam – poprawna forma czasownika  Nie wiadomo czy niewiadomo – zasady poprawnej pisowni
Nie wiadomo czy niewiadomo – zasady poprawnej pisowni  Z pod czy spod – poprawny zapis w języku polskim
Z pod czy spod – poprawny zapis w języku polskim  Oliwii czy oliwi – jak poprawnie pisać imię?
Oliwii czy oliwi – jak poprawnie pisać imię?  Kalkulator dat – różnica dni i terminy
Kalkulator dat – różnica dni i terminy  Huczy czy chuczy – jak to napisać?
Huczy czy chuczy – jak to napisać?  Kalkulator godzin – czas pracy i nadgodziny
Kalkulator godzin – czas pracy i nadgodziny  Kalkulator metrów kwadratowych – szybkie obliczanie powierzchni
Kalkulator metrów kwadratowych – szybkie obliczanie powierzchni  Kalkulator kredytu hipotecznego – rata, zdolność, koszty
Kalkulator kredytu hipotecznego – rata, zdolność, koszty  Kalkulator odsetek podatkowych – ile musisz dopłacić?
Kalkulator odsetek podatkowych – ile musisz dopłacić?  Strona bierna angielski ćwiczenia – praktyczne zadania z odpowiedziami
Strona bierna angielski ćwiczenia – praktyczne zadania z odpowiedziami  Kalkulator frekwencji – oblicz swoją obecność
Kalkulator frekwencji – oblicz swoją obecność  Perfum czy perfuma – jaka liczba jest poprawna?
Perfum czy perfuma – jaka liczba jest poprawna?  Hanie czy Hanię – jak poprawnie odmieniać imię?
Hanie czy Hanię – jak poprawnie odmieniać imię?  Niemniej czy nie mniej – kiedy którą formę stosować?
Niemniej czy nie mniej – kiedy którą formę stosować?  Kornelii czy Korneli – jak odmieniać to imię?
Kornelii czy Korneli – jak odmieniać to imię?  Wymyślić czy wymyśleć – poprawna forma czasownika
Wymyślić czy wymyśleć – poprawna forma czasownika  Maji czy mai – która forma jest poprawna?
Maji czy mai – która forma jest poprawna?  Ani czy Anii – poprawna odmiana imienia
Ani czy Anii – poprawna odmiana imienia  Darii czy Dari – jak poprawnie odmieniać imię?
Darii czy Dari – jak poprawnie odmieniać imię?  Tempo czy tępo – która pisownia jest właściwa?
Tempo czy tępo – która pisownia jest właściwa?  Pokolei czy po kolei – jak to zapisać?
Pokolei czy po kolei – jak to zapisać?  Wyzwania w doskonaleniu zawodowym nauczycieli
Wyzwania w doskonaleniu zawodowym nauczycieli  Co to jest nauczanie hybrydowe i jak działa?
Co to jest nauczanie hybrydowe i jak działa?  Czy woda przewodzi prąd – proste wyjaśnienie dla uczniów
Czy woda przewodzi prąd – proste wyjaśnienie dla uczniów  Wzór na deltę – jak obliczyć deltę krok po kroku
Wzór na deltę – jak obliczyć deltę krok po kroku  Jak przejść na nauczanie domowe?
Jak przejść na nauczanie domowe?  Musiałbym czy musiał bym – razem czy osobno?
Musiałbym czy musiał bym – razem czy osobno?  Jak skutecznie uczyć się języka niemieckiego, aby szybko zrobić postępy?
Jak skutecznie uczyć się języka niemieckiego, aby szybko zrobić postępy?  Kiedy liczba jest podzielna przez 12 – prosty sposób na sprawdzenie
Kiedy liczba jest podzielna przez 12 – prosty sposób na sprawdzenie  Zł z kropką czy bez – poprawny zapis kwot w złotówkach
Zł z kropką czy bez – poprawny zapis kwot w złotówkach  Hamak czy chamak – poprawna pisownia i wyjaśnienie
Hamak czy chamak – poprawna pisownia i wyjaśnienie  Twierdzenie Talesa – zadania z rozwiązaniami
Twierdzenie Talesa – zadania z rozwiązaniami  Jak napisać email po angielsku – praktyczny poradnik krok po kroku
Jak napisać email po angielsku – praktyczny poradnik krok po kroku  Czy egzamin wewnętrzny praktyczny jest obowiązkowy?
Czy egzamin wewnętrzny praktyczny jest obowiązkowy?  Skutki cyber przemocy – konsekwencje dla uczniów
Skutki cyber przemocy – konsekwencje dla uczniów  Model komórki zwierzęcej – jak zrobić krok po kroku?
Model komórki zwierzęcej – jak zrobić krok po kroku?  Jak zrobić instrument muzyczny do szkoły – pomysły DIY dla uczniów
Jak zrobić instrument muzyczny do szkoły – pomysły DIY dla uczniów  Ułamki zwykłe – ćwiczenia do wydruku dla uczniów szkoły podstawowej
Ułamki zwykłe – ćwiczenia do wydruku dla uczniów szkoły podstawowej  Jak obliczyć średnią na studiach – skala ocen i wzory
Jak obliczyć średnią na studiach – skala ocen i wzory  Czy warto inwestować w kursy matematyczne w dobie darmowych materiałów w sieci?
Czy warto inwestować w kursy matematyczne w dobie darmowych materiałów w sieci?  Dysonans poznawczy – co to jest i skąd się bierze?
Dysonans poznawczy – co to jest i skąd się bierze?  To be – ćwiczenia PDF do samodzielnej nauki
To be – ćwiczenia PDF do samodzielnej nauki  Past perfect vs past simple – różnice i przykłady użycia
Past perfect vs past simple – różnice i przykłady użycia  Życzenia urodzinowe dla babci – piękne słowa prosto z serca
Życzenia urodzinowe dla babci – piękne słowa prosto z serca  Dzieje Tristana i Izoldy – streszczenie z omówieniem
Dzieje Tristana i Izoldy – streszczenie z omówieniem  Chłopi – streszczenie szczegółowe lektury
Chłopi – streszczenie szczegółowe lektury  Na pewno – razem czy oddzielnie w poprawnej polszczyźnie?
Na pewno – razem czy oddzielnie w poprawnej polszczyźnie?  Energa24 logowanie – jak szybko zalogować się do eBOK?
Energa24 logowanie – jak szybko zalogować się do eBOK?  Od razu – razem czy osobno i dlaczego?
Od razu – razem czy osobno i dlaczego?  Po prostu – razem czy osobno w języku polskim?
Po prostu – razem czy osobno w języku polskim?  Wzór na objętość sześcianu – proste wyjaśnienie
Wzór na objętość sześcianu – proste wyjaśnienie  Chojnie czy hojnie – jak piszemy to słowo?
Chojnie czy hojnie – jak piszemy to słowo?  Czy po technikum można iść na studia?
Czy po technikum można iść na studia?